Codeforces Round #603 (Div. 2)- E Editor
概要
無限に長い配列がある。カーソルが存在していて、最初は1文字目を指す。
あなたはつぎのような操作を行える
- カーソルを一つ右に動かす。
- カーソルを一つ左に動かす。ただし、一番左ならば何も起きない。
- カーソルの指してる配列の文字を特定の文字で上書きする。ただし、その特定の文字は小文字アルファベットと'(' and ')'。
右に動かす操作を'R', 左に動かす操作を'L'、特定の文字で上書きするのを「上書きする文字」であらわす(pで配列の中身を上書きするのなら、'p')と、操作を1文字にする。
この一つ一つの操作をまとめた長さNの操作列が与えられる。
一つの操作を終えるごとに、現在配列に入ってる文字列の () の深さを答えよ。()の整合が取れてないのならば、-1と答えよ。
例えば、"ab(a(f)ff)()(s)"はかっこ列の深さとしては2であり、"(a()st)(s"はかっこの整合が取れてないので、-1となる。
制約:
1 <<= N <= 10^6
ACするまで
1. かっこ列の深さは、 '(' が出たら +1, ')'が出たら -1と左から累積和を取ってその最大値である。整合性の条件は、最後で'('の数と')'の数が同じで、途中必ず、どこでも'('の数は')'の数以上、である。これを踏まえて考える。
2. 1回の操作を終えるたびに、全体の累積和配列の最大値、最小値と累積和の最後の結果が分かればよい。これって、データ構造じゃね?
3. 遅延セグメント木を使えば、区間加算と区間のMax, Minが計算できるので実装してみる。->TLE
4. 計算量的には問題がないはず。問題の操作列を先読みして定数倍高速化してAC!
考察
力技
()列の深さ、整合性の問題は、前から見て'('があったら+1, ')'があったら-1をするように累積和を取ればよい。(後ろから'('があったら-1, ')'があったら+1をするように累積和を取ってもいい)。そして、その途中で累積和が常に正であり、最後では必ず0になることが整合のとれたかっこ列の条件である。
今回は、操作ごとに、かっこ列の深さとかっこ列として正しいかどうかについて判断するので、必要な情報は、
- 編集中の文字列の累積和の最大値(現在編集中の文字列の最も深いかっこの深さに該当する)
- 累積和の最小値(0未満ならば、整合のとれた()列ではないということ)
- 最後までの累積和('('の数と')'の数が一致してるかどうか)
である。
これは、遅延セグメント木を使用すれば、文字の書き換えごとに、累積和配列の更新を[更新地点, 最後)までの区間加算クエリとしてみなせるので、区間加算が可能で、区間の最大値、最小値が求められるような遅延セグメント木を実装すればよい。計算量はO(N log N)。
ちなみに、beetさんの遅延セグ木は、モノイドと単位元と作用素を渡すだけで簡単にこれを実現できるようになってる。beetさんモデルの遅延セグメント木おすすめ。
beetさんの記事:
beet-aizu.hatenablog.com
ちなみに、そのまま実装すると、N <= 10^6なので微妙にTLEする。
ここで、与えられる配列の長さの最大は、Nではなく操作列の中で出てきたRの回数であることに着目して、定数倍高速化すれば通る。
解説解
このようなカーソルをもって、左右に分割して、1回の操作でたかだか1つしか変動しないのは、前半と後半を受けもつ2つのデータ構造に分けて、その差分だけ更新するとうまくいくことが多い。
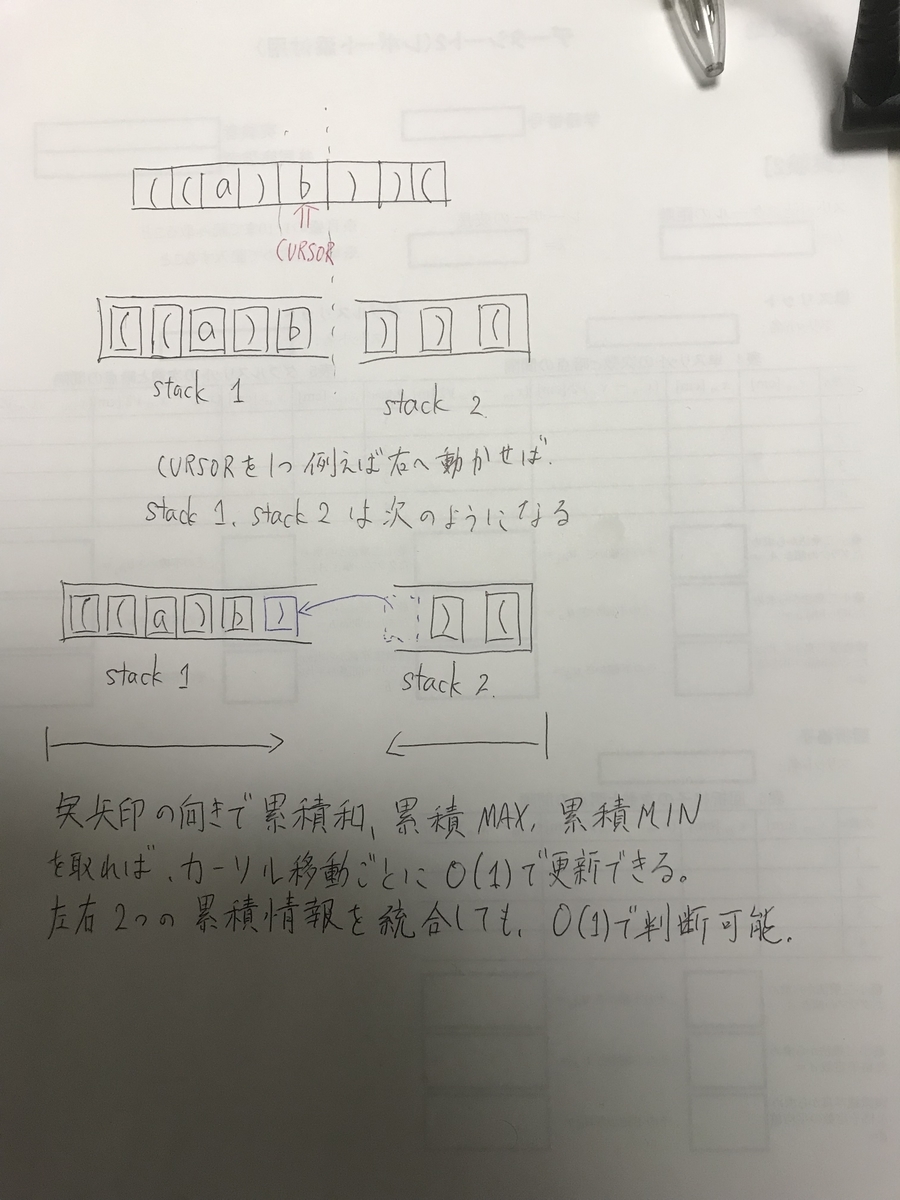
今回の場合は、stackを使用して上のようにすればよい。
2つのデータ構造で1つの実変動する場合の差分を変更するのは、ABC127-F Absolute Minimaに似ている。(総集記事書く予定)
一言
実装力がつきそうな問題だった。